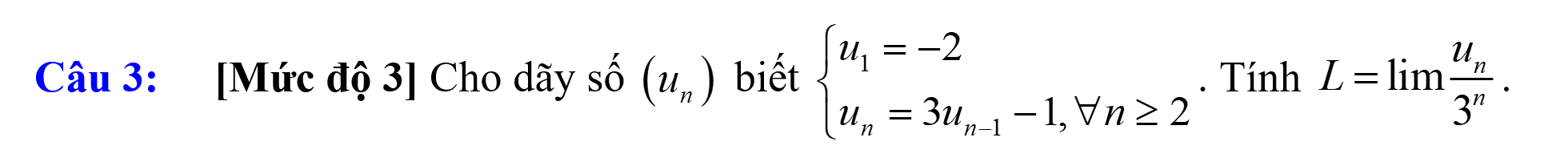Toán lớp 11 giới hạn dãy số học kỳ 1
Đề bài:
Cho dãy số 
biết:
![\[\begin{cases} u_1 = -2 \ u_n = 3u_{n-1} - 1, \quad \forall n \geq 2 \end{cases}\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-c4dd6e8326e438a4ae8bf9ac1c4955d6_l3.png "Rendered by QuickLaTeX.com")
Tính giới hạn
.
Lời giải chi tiết
Bước 1: Tìm công thức tổng quát của 
Dãy số được cho bởi công thức truy hồi 
. Đây là dạng dãy số 
với 
và 
.
Để tìm công thức tổng quát, ta tìm điểm bất động 
sao cho 
.
![\[c = 3c - 1\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-c819d24a41486876c4e8cf91b13289de_l3.png "Rendered by QuickLaTeX.com")
![\[1 = 2c\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-0885992f9539d2a87d2f20152f8a3fa1_l3.png "Rendered by QuickLaTeX.com")
![\[c = \frac{1}{2}\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-1e5b58910ee21d4bf74233331a347906_l3.png "Rendered by QuickLaTeX.com")
Đặt 
. Khi đó, 
.
Thay vào công thức truy hồi:
![\[v_n + \frac{1}{2} = 3 \left( v_{n-1} + \frac{1}{2} \right) - 1\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-ca6c3654b7b86f7988dd1657dd68b104_l3.png "Rendered by QuickLaTeX.com")
![\[v_n + \frac{1}{2} = 3v_{n-1} + \frac{3}{2} - 1\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-2f145c1bf8db5d2c5764d62e1ad64f8a_l3.png "Rendered by QuickLaTeX.com")
![\[v_n + \frac{1}{2} = 3v_{n-1} + \frac{1}{2}\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-f97c1d0f0147134549bf5dee51714e8e_l3.png "Rendered by QuickLaTeX.com")
![\[v_n = 3v_{n-1}\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-0af0eee6764ca6922727ea9868904a6a_l3.png "Rendered by QuickLaTeX.com")
Dãy số 
là cấp số nhân với công bội 
.
Bước 2: Xác định số hạng đầu của 
Ta có 
.
Vì 
, ta có:
![\[v_1 = -2 - \frac{1}{2} = -\frac{5}{2}\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-1076aa9d4dd0da0ff74c637bb6413583_l3.png "Rendered by QuickLaTeX.com")
Bước 3: Viết công thức tổng quát cho
Công thức tổng quát của cấp số nhân là:
![\[v_n = v_1 \cdot q^{n-1} = -\frac{5}{2} \cdot 3^{n-1}\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-9002d1293de2d2d451248d8c8cfbabfd_l3.png "Rendered by QuickLaTeX.com")
Do , ta suy ra công thức tổng quát của :
![\[u_n = -\frac{5}{2} \cdot 3^{n-1} + \frac{1}{2}\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-e21f8e2937d20b02402ba43886696046_l3.png "Rendered by QuickLaTeX.com")
Bước 4: Tính giới hạn 
Ta cần tính .
Thay công thức vừa tìm được vào biểu thức giới hạn:
![\[L = \lim_{n \to \infty} \frac{-\frac{5}{2} \cdot 3^{n-1} + \frac{1}{2}}{3^n}\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-b2e6e3d68eb8bcf47493e869157ba491_l3.png "Rendered by QuickLaTeX.com")
Ta biến đổi 
về dạng có chứa 
:
![\[-\frac{5}{2} \cdot 3^{n-1} = -\frac{5}{2} \cdot \frac{3^n}{3} = -\frac{5}{6} \cdot 3^n\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-f52896775f597194eb7458511556e99d_l3.png "Rendered by QuickLaTeX.com")
Thay lại vào biểu thức giới hạn :
![\[L = \lim_{n \to \infty} \frac{-\frac{5}{6} \cdot 3^n + \frac{1}{2}}{3^n}\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-f30151c415ae69f4faa0cfdee98aaad1_l3.png "Rendered by QuickLaTeX.com")
Chia cả tử và mẫu cho :
![\[L = \lim_{n \to \infty} \left( \frac{-\frac{5}{6} \cdot 3^n}{3^n} + \frac{\frac{1}{2}}{3^n} \right)\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-59e020d84e35248ba04432d8a4952d5b_l3.png "Rendered by QuickLaTeX.com")
![\[L = \lim_{n \to \infty} \left( -\frac{5}{6} + \frac{1}{2 \cdot 3^n} \right)\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-2d5e0fb4e0bf59c7444d59a97f349807_l3.png "Rendered by QuickLaTeX.com")
Khi 
, ta có 
, do đó 
.
Vậy:
![\[L = -\frac{5}{6} + 0\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-4ba586e869b7bf636d0660de9e3398e9_l3.png "Rendered by QuickLaTeX.com")
![\[L = -\frac{5}{6}\]](https://wordtoan.com/wp-content/ql-cache/quicklatex.com-f589ab1bf41ea20b92c71a8b49f9ddce_l3.png "Rendered by QuickLaTeX.com")
Kết luận:
Giới hạn cần tìm là:
