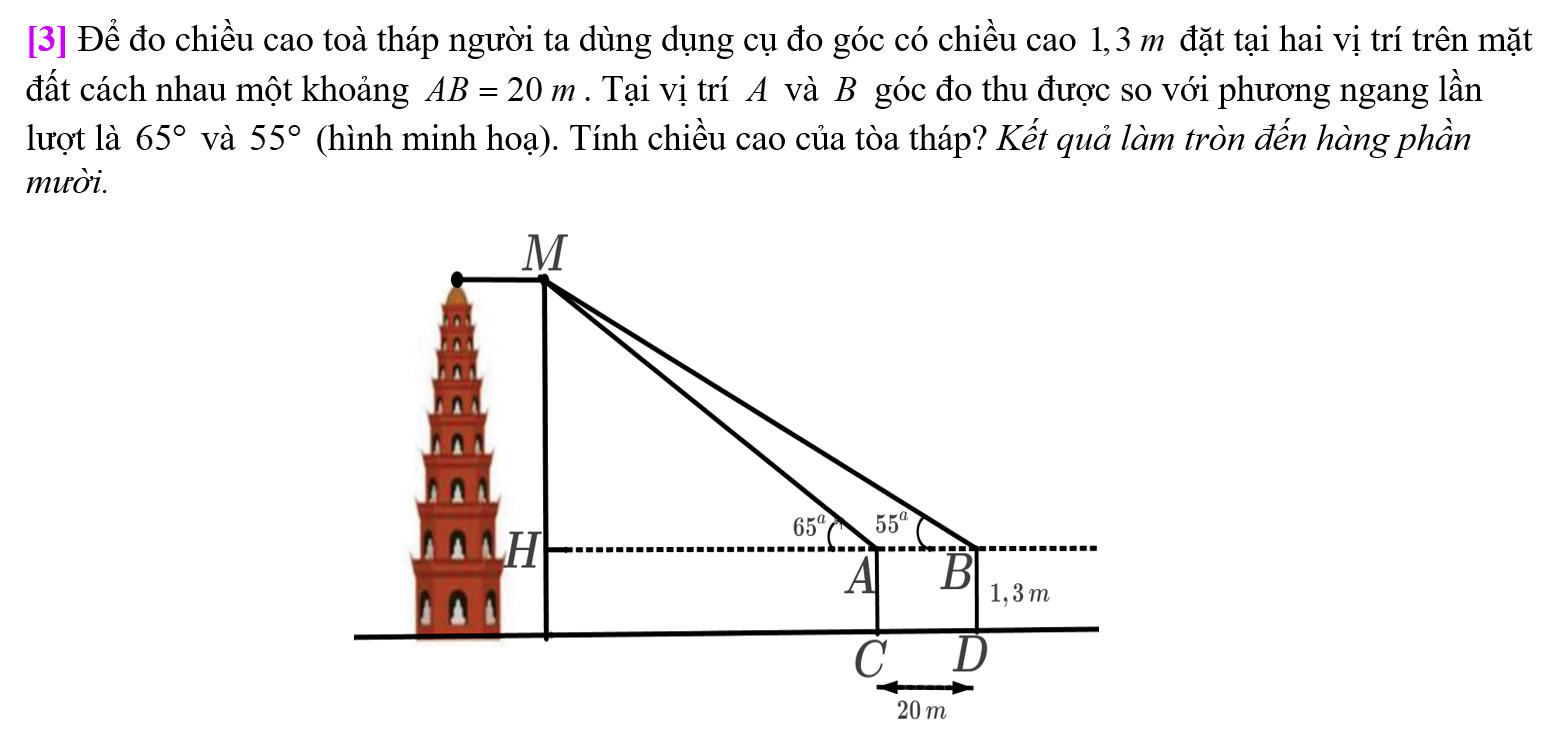
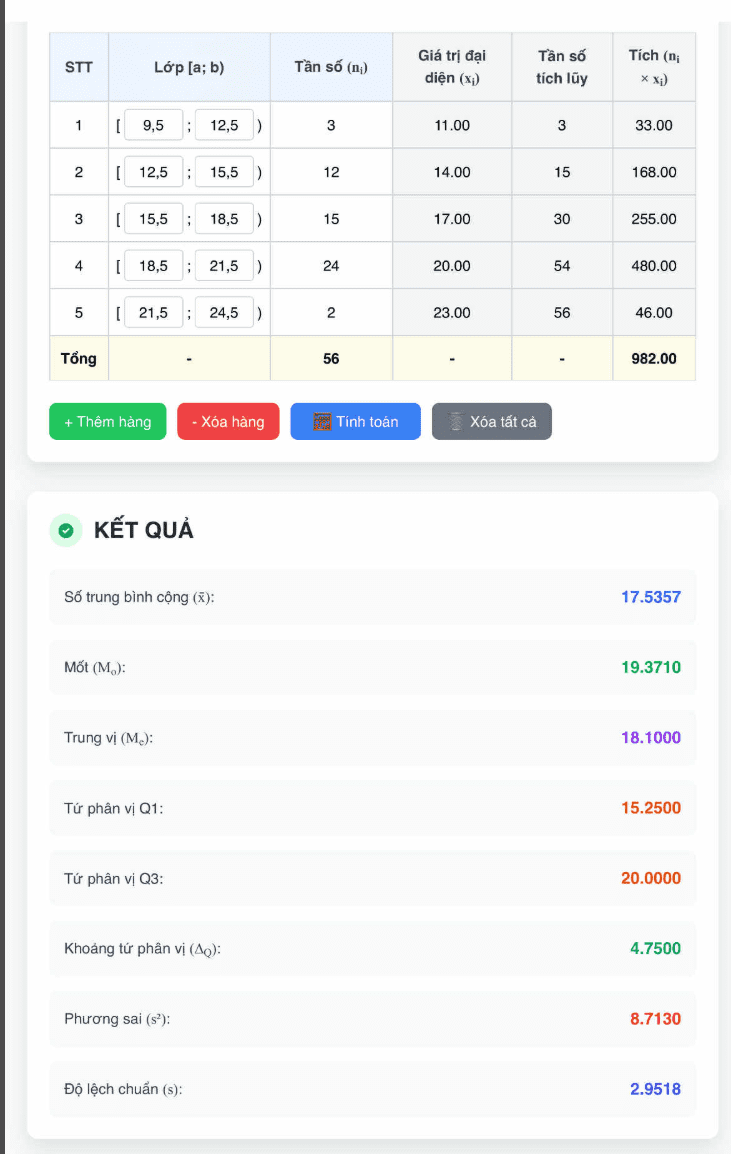
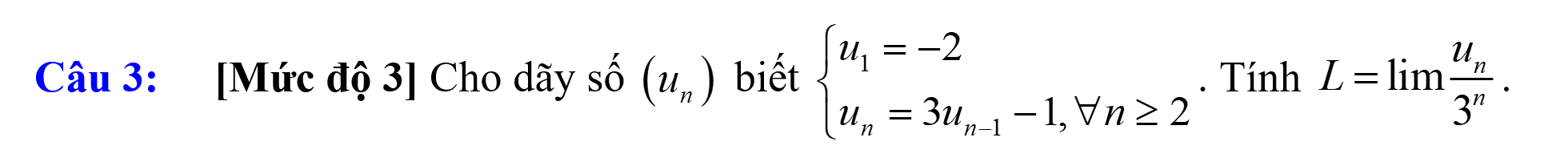Đề cuối kỳ 1 Toán 11 năm 2025 2026 trường THCS-THPT Diên Hồng Thành Phố Hồ Chí Minh

KIỂM TRA CUỐI HỌC KỲ I – MÔN TOÁN LỚP 11

PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN (4 điểm)

Câu 1. Đổi số đo của góc $1983^\circ$ sang rad ta được

$\text{rad} = 1983^\circ \cdot \frac{\pi}{180} = \frac{1983}{180} \pi$

Rút gọn phân số (chia cả tử và mẫu cho 3):

$\frac{1983}{180} \pi = \frac{661}{60} \pi$

Đáp án: D.

Câu 2. Tính giới hạn $\lim_{n \to \infty} \frac{n+1}{2n+4}$
Chia cả tử và mẫu cho $n$ :

$\lim_{n \to \infty} \frac{n+1}{2n+4} = \lim_{n \to \infty} \frac{1 + \frac{1}{n}}{2 + \frac{4}{n}} = \frac{1+0}{2+0} = \frac{1}{2}$

Đáp án: B.

Câu 3. Tìm tập xác định $D$ của hàm số $y = \frac{2023}{\sin x}$
Điều kiện để hàm số xác định là mẫu số khác 0: $\sin x \neq 0$ .
$\sin x = 0$ khi $x = k\pi, k \in \mathbb{Z}$ .
Vậy $D = \mathbb{R} \setminus {k\pi, k \in \mathbb{Z}}$ .
Đáp án: B.

Câu 4. Dãy số nào sau đây là một cấp số cộng?
Ta kiểm tra công sai $d = u_{n+1} - u_n$ phải là hằng số.
D. $-3, -6, -9, -12$ .
$d_1 = -6 - (-3) = -3$ .
$d_2 = -9 - (-6) = -3$ .
$d_3 = -12 - (-9) = -3$ .
Dãy số này là cấp số cộng với $d=-3$ .
Đáp án: D.

Câu 5. Tìm tập nghiệm của phương trình $\cos(-2x) = \cos \frac{\pi}{6}$
Ta có $\cos(-2x) = \cos(2x)$ . Phương trình trở thành $\cos(2x) = \cos \frac{\pi}{6}$ .

$\begin{cases} 2x = \frac{\pi}{6} + k2\pi \ 2x = -\frac{\pi}{6} + k2\pi \end{cases} \quad (k \in \mathbb{Z})$

Chia cả hai vế cho 2:

$x = \frac{\pi}{12} + k\pi \quad \text{hoặc} \quad x = -\frac{\pi}{12} + k\pi, \quad k \in \mathbb{Z}$

Nếu sử dụng ký hiệu $k\pi$ thay vì $-k\pi$ (vì $k \in \mathbb{Z}$ ):

$S = \left{\frac{1}{12}\pi + k\pi, -\frac{1}{12}\pi + k\pi \mid k \in \mathbb{Z}\right}$

Đối chiếu với đáp án B (sử dụng $-k\pi$ ): $S=\left{\frac{1}{12}\pi - k\pi, -\frac{1}{12}\pi - k\pi \mid k \in \mathbb{Z}\right}$ . Hai tập hợp này là như nhau.
Đáp án: B.

Câu 6. Cho tứ diện $ABCD$ có $M, N$ lần lượt là trung điểm của $AB, AC$ . Mặt phẳng nào sau đây song song với đường thẳng $MN$ ?
Trong $\triangle ABC$ , $MN$ là đường trung bình, suy ra $MN \parallel BC$ .
Vì $BC \subset (BCD)$ và $MN$ không nằm trong $(BCD)$ , nên $MN \parallel (BCD)$ .
Đáp án: D.

Câu 7. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$ . Giao tuyến của mặt phẳng $(SAC)$ và mặt phẳng $(SBD)$ là
Hai mặt phẳng có điểm chung $S$ và điểm chung $O = AC \cap BD$ .
Giao tuyến là đường thẳng $SO$ .
Đáp án: B.

Câu 8. Cho dãy số $(u_n)$ có $u_n = \frac{5}{n+5}$ . Tính $u_{15}$ ?
Thay $n=15$ :

$u_{15} = \frac{5}{15+5} = \frac{5}{20} = \frac{1}{4}$

Đáp án: A.

Câu 9. Tính giới hạn $\lim_{x \to 2} \frac{3x^2 - 4x - 4}{4x - 8}$
Đây là dạng $\frac{0}{0}$ . Ta phân tích nhân tử:

$\lim_{x \to 2} \frac{(x-2)(3x + 2)}{4(x-2)} = \lim_{x \to 2} \frac{3x + 2}{4}$

Thay $x=2$ :

$= \frac{3(2) + 2}{4} = \frac{8}{4} = 2$

Đáp án: A.

Câu 10. Cho $(\alpha) \parallel (\beta)$ . Khẳng định nào sau đây là đúng?
Hai mặt phẳng song song thì không có điểm chung.
Đáp án: D.

Câu 11. Trên đường tròn có bán kính $R=3$ . Tính độ dài cung có số đo $1$ radian trên đường tròn?
Công thức độ dài cung $l = R \cdot \alpha$ .

$l = 3 \cdot 1 = 3$

Đáp án: A.

Câu 12. Cho cấp số nhân $(u_n)$ có số hạng đầu $u_1 = 4$ , công bội $q = -3$ . Tính $u_{11}$ .

$u_{11} = u_1 \cdot q^{10} = 4 \cdot (-3)^{10} = 4 \cdot 59049 = 236196$

Đáp án: B.

Câu 13. Đẳng thức nào sau đây là đúng với $\forall a \neq \frac{\pi}{2} + k\pi; k \in \mathbb{Z}$ ?
Đẳng thức lượng giác cơ bản: $1 + \tan^2 a = \frac{1}{\cos^2 a}$ .
Đáp án: D.

Câu 14. Tìm giá trị lớn nhất của hàm số $y = 10 \cos(2x) + 2$ .
Ta có $-1 \leq \cos(2x) \leq 1$ .

$y_{max} = 10 \cdot 1 + 2 = 12$

Đáp án: A.

Câu 15. Cho $\frac{\pi}{2} < x < \pi$ . Chọn phát biểu sai trong các phát biểu sau?
Trong góc phần tư thứ II: $\sin x > 0$ , $\cos x < 0$ , $\tan x < 0$ , $\cot x < 0$ . Phát biểu D ( $\cot x > 0$ ) là sai.
Đáp án: D.

Câu 16. Có bao nhiêu hàm số lẻ trong các hàm số $y = \sin x; y = \cos x; y = \tan x$ và $y = \cot x$ .
Các hàm số lẻ: $y=\sin x$ , $y=\tan x$ , $y=\cot x$ . (3 hàm)
Đáp án: C.

PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI (3 điểm)

Câu 1. Cho cấp số cộng $(u_n)$ có $u_2 = -10; u_4 = -18$ .

Giải:
Ta có $u_4 - u_2 = (u_1 + 3d) - (u_1 + d) = 2d$ .
$2d = -18 - (-10) = -8 \implies d = -4$ .
$u_1 = u_2 - d = -10 - (-4) = -6$ .
Số hạng tổng quát: $u_n = -6 + (n-1)(-4) = -4n - 2$ .

a) Số hạng đầu của cấp số cộng là $u_1 = -4$ . (S) (Đúng là $u_1 = -6$ )
b) Số hạng thứ 8 của cấp số cộng là $u_8 = -38$ .
$u_8 = -4(8) - 2 = -32 - 2 = -34$ . (S)
c) Số $-114$ là một số hạng của cấp số cộng.
$u_n = -114 \implies -4n - 2 = -114 \implies -4n = -112 \implies n = 28$ . (Đ)
d) Tổng 8 số hạng đầu của cấp số cộng là $S_8 = -156$ .
$S_8 = \frac{8(u_1 + u_8)}{2} = 4(-6 + (-34)) = 4(-40) = -160$ . (S)

Câu 2. Cho biết $\sin \alpha = \frac{3}{5}, \frac{\pi}{2} < \alpha < \pi$ .
Góc $\alpha$ nằm trong góc phần tư thứ II, nên $\cos \alpha < 0$ và $\tan \alpha < 0$ .
Ta có $\cos^2 \alpha = 1 - \left(\frac{3}{5}\right)^2 = \frac{16}{25}$ . Do $\cos \alpha < 0$ , nên $\cos \alpha = -\frac{4}{5}$ .
$\tan \alpha = \frac{\sin \alpha}{\cos \alpha} = \frac{3/5}{-4/5} = -\frac{3}{4}$ .

a) $\cos \alpha > 0$ . (S) (Đúng là $\cos \alpha < 0$ )
b) $\cos \alpha = \frac{4}{5}$ . (S) (Đúng là $\cos \alpha = -\frac{4}{5}$ )
c) $\tan \alpha = \frac{3}{4}$ . (S) (Đúng là $\tan \alpha = -\frac{3}{4}$ )
d) $\tan\left(\alpha + \frac{\pi}{4}\right) = \frac{48 - 25\sqrt{3}}{11}$ .
$\tan\left(\alpha + \frac{\pi}{4}\right) = \frac{\tan \alpha + \tan \frac{\pi}{4}}{1 - \tan \alpha \tan \frac{\pi}{4}} = \frac{-3/4 + 1}{1 - (-3/4)(1)} = \frac{1/4}{7/4} = \frac{1}{7}$ . (S)

Câu 3. Cho hàm số $f(x) = \begin{cases} \frac{x^2 + 4x - 12}{x^2 - 4} & \text{khi } x > 2 \ x & \text{khi } x \leq 2 \end{cases}$

a) $f(2)=2$ .
Vì $2 \leq 2$ , ta dùng công thức $f(x)=x$ . $f(2) = 2$ . (Đ)
b) $f(3) = \frac{4}{5}$ .
Vì $3 > 2$ , ta dùng công thức trên: $f(3) = \frac{3^2 + 4(3) - 12}{3^2 - 4} = \frac{9+12-12}{9-4} = \frac{9}{5}$ . (S)
c) Hàm số $f(x)$ liên tục tại $x = 3$ .
Tại $x=3$ , $f(x)$ là hàm phân thức xác định, nên liên tục. (Đ)
d) Hàm số $f(x)$ không liên tục tại $x = 2$ .
Ta tính giới hạn tại $x=2$ :
$\lim_{x \to 2^-} f(x) = \lim_{x \to 2^-} x = 2$ .
$\lim_{x \to 2^+} f(x) = \lim_{x \to 2^+} \frac{(x-2)(x+6)}{(x-2)(x+2)} = \lim_{x \to 2^+} \frac{x+6}{x+2} = \frac{8}{4} = 2$ .
Vì $\lim_{x \to 2^-} f(x) = \lim_{x \to 2^+} f(x) = f(2) = 2$ , hàm số liên tục tại $x=2$ . (S)

PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN (1.5 điểm)

Câu 1. Giá trị còn lại của chiếc xe sau 4 năm sử dụng.
Giá ban đầu $P_0 = 870$ (triệu đồng).
Giá trị giảm sau 4 năm: $4 \times 40 = 160$ (triệu đồng).
Giá trị còn lại: $870 - 160 = 710$ (triệu đồng).
Đáp số: 710

Câu 2. Tổng số tiền phải thanh toán để khoan giếng sâu 20 mét.
Đây là cấp số cộng với $u_1 = 200,000$ và $d = 30,000$ . $n=20$ .
Số tiền cho mét thứ 20 ( $u_{20}$ ):

$u_{20} = u_1 + 19d = 200,000 + 19 \cdot 30,000 = 200,000 + 570,000 = 770,000 \text{ (đồng)}$

Tổng số tiền $S_{20}$ :

$S_{20} = \frac{20(u_1 + u_{20})}{2} = 10(200,000 + 770,000) = 10(970,000) = 9,700,000 \text{ (đồng)}$

Đổi sang triệu đồng và làm tròn đến hàng phần chục:

$S_{20} = 9.7 \text{ triệu đồng}$

Đáp số: 9.7

Câu 3. Tìm thời điểm $t$ nào thì $s = \sqrt{3}$ (cm) trong 0.2 giây đầu.
Ta giải phương trình $2 \sin\left(2t + \frac{\pi}{4}\right) = \sqrt{3}$ :

$\sin\left(2t + \frac{\pi}{4}\right) = \frac{\sqrt{3}}{2}$

$\begin{cases} 2t + \frac{\pi}{4} = \frac{\pi}{3} + k2\pi \ 2t + \frac{\pi}{4} = \pi - \frac{\pi}{3} + k2\pi = \frac{2\pi}{3} + k2\pi \end{cases}$

$2t = \frac{\pi}{12} + k2\pi \implies t = \frac{\pi}{24} + k\pi$
$2t = \frac{5\pi}{12} + k2\pi \implies t = \frac{5\pi}{24} + k\pi$

Vì $t \in (0, 0.2]$ .
Xét trường hợp 1: Với $k=0$ , $t_1 = \frac{\pi}{24} \approx 0.1309$ (thỏa mãn $0.1309 \leq 0.2$ ).
Xét trường hợp 2: Với $k=0$ , $t_2 = \frac{5\pi}{24} \approx 0.6545$ (loại).
Thời điểm cần tìm là $t = \frac{\pi}{24} \text{ s}$ .
Làm tròn đến hàng phần trăm: $t \approx 0.13 \text{ s}$ .
Đáp số: 0.13

PHẦN IV. TỰ LUẬN (1.5 điểm)

Câu 1. Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O$ . Gọi $M, N$ lần lượt là trung điểm của $SD, CD$ .

a/ Tìm giao tuyến của hai mặt phẳng $(SAC)$ và $(SBD)$ .

$S$ là điểm chung hiển nhiên.
Vì $ABCD$ là hình bình hành tâm $O$ , nên $O$ là giao điểm của hai đường chéo $AC$ và $BD$ .
$O \in AC \subset (SAC)$ và $O \in BD \subset (SBD)$ .
Vậy $O$ là điểm chung thứ hai.
Giao tuyến của $(SAC)$ và $(SBD)$ là đường thẳng $SO$ .

b/ Tìm giao tuyến của hai mặt phẳng $(SAB)$ và $(SCD)$ .

$S$ là điểm chung hiển nhiên.
Đáy $ABCD$ là hình bình hành nên $AB \parallel CD$ .
Ta có $AB \subset (SAB)$ , $CD \subset (SCD)$ , và $AB \parallel CD$ .
Theo định lý về giao tuyến của hai mặt phẳng chứa hai đường thẳng song song, giao tuyến là đường thẳng $d$ đi qua $S$ và $d \parallel AB \parallel CD$ .

c/ Tìm giao điểm của đường thẳng $BM$ và mặt phẳng $(SAC)$ .
Gọi $I$ là giao điểm cần tìm.

Chọn mặt phẳng phụ chứa $BM$ : $(SBD)$ .
Tìm giao tuyến của mặt phẳng phụ $(SBD)$ và $(SAC)$ là $SO$ (theo câu a).
Trong mặt phẳng $(SBD)$ , gọi $I = BM \cap SO$ .
Vì $I \in SO$ và $SO \subset (SAC)$ , nên $I$ là giao điểm của $BM$ và $(SAC)$ .
Nhận xét thêm: $I$ là trọng tâm của $\triangle SBD$ (do $O$ là trung điểm $BD$ , $M$ là trung điểm $SD$ ).

d/ Chứng minh mặt phẳng $(SBC)$ song song với mặt phẳng $(OMN)$ .
Ta chứng minh hai đường thẳng cắt nhau trong $(OMN)$ song song với $(SBC)$ .

Xét đường thẳng $MN$ :
$M$ là trung điểm $SD$ , $N$ là trung điểm $CD$ .
Trong $\triangle SCD$ , $MN$ là đường trung bình $\implies MN \parallel SC$ .
Vì $SC \subset (SBC)$ và $MN \not\subset (SBC)$ , suy ra $MN \parallel (SBC)$ .
Xét đường thẳng $ON$ :
$O$ là trung điểm $BD$ , $N$ là trung điểm $CD$ .
Trong $\triangle BCD$ , $ON$ là đường trung bình $\implies ON \parallel BC$ .
Vì $BC \subset (SBC)$ và $ON \not\subset (SBC)$ , suy ra $ON \parallel (SBC)$ .
Ta có $MN$ và $ON$ là hai đường thẳng cắt nhau tại $N$ trong $(OMN)$ , và cả hai đều song song với $(SBC)$ .
Vậy, mặt phẳng $(OMN)$ song song với mặt phẳng $(SBC)$ .